„Tai yra visiškai nauja ir kur kas paprasčiau nei bet kas, kas buvo padaryta iki šiol“, - sakė Oksfordo universiteto (Jungtinė Karalystė) fizikas-matematikas Andrew Hodgesas, stebėjęs darbo eigą.
Atradimas, kad dalelių sąveika – patys paprasčiausi gamtoje pasitaikantys įvykiai – gali būti geometrijos pasekmė, gerokai į priekį pastumia dešimtmečius trunkančius darbus siekiant performuluoti kvantinio laiko teoriją – dėsnių rinkinį, aprašantį elementariąsias daleles ir jų sąveikas. Sąveikos, kurios anksčiau buvo aprašinėjamos tūkstančių išraiškų ilgio matematinėmis formulėmis, dabar gali būti aprašomos apskaičiuojant deimantą primenančio hipotetinio matematinio objekto „amplituedro“ tūrį – šių skaičiavimų aprašymas telpa į vieną matematinę išraišką, rašo simonsfoundation.org.
„Efektyvumo laipsnis tiesiog stulbinantis. Dabar popieriuje bus galima be problemų atlikti skaičiavimus, kurie iki šiol buvo sunkiai įkandami kompiuteriams“, - sakė Harvardo universiteto (JAV) fizikas teoretikas Jacobas Bourjaily, vienas iš naujosios idėjos vystytojų.
Nauja geometrinė kvantinio lauko teorijos versija taip pat palengvina ir kvantinės gravitacijos teorijos paieškas – ji turėtų sujungti Visatos dideliu masteliu ir Visatos mažu masteliu aprašymus. Visi ligšioliniai bandymai įtraukti gravitaciją į fizikos dėsnius kvantiniame lygmenyje atsimušdavo į nesąmoningų begalybių ir paradoksų sieną. Amplituedras arba panašus geometrinis objektas galėtų teoretikams padėti atsisakyti dviejų giliai įsišaknijusių fizikos principų: lokalumo ir unitariškumo.
„Abu jie labai glaudžiai susieti su mūsų įprastiniu būdu galvoti apie daiktus. Abu yra įtariamieji“, - sakė pažangiųjų tyrimų instituto (JAV) profesorius Nima Arkani-Hamedas, vadovaujantis šiam darbui, kuris yra pristatinėjamas įvairiose konferencijose ir netrukus bus aprašytas moksliniame straipsnyje.
Lokalumas – tai suvokimas, jog dalelės gali sąveikauti tik sutapus jų pozicijoms laike ir erdvėje. Unitariškumas teigia, kad visų kvantinės mechanikos sąveikų tikimybių suma turi būti vienetas. Abi šios sąvokos yra pagrindinės kvantinio lauko teorijos kolonos, tačiau tam tikrose situacijose, kuomet kalbama apie gravitaciją, abu šie principai griūva. Tai verčia manyti, kad nė vienas iš jų nėra fundamentali gamtos savybė.
 Efektyvumo laipsnis tiesiog stulbinantis. Dabar popieriuje bus galima
be problemų atlikti skaičiavimus, kurie iki šiol buvo sunkiai įkandami
kompiuteriams
Efektyvumo laipsnis tiesiog stulbinantis. Dabar popieriuje bus galima
be problemų atlikti skaičiavimus, kurie iki šiol buvo sunkiai įkandami
kompiuteriams
„Tai geresnis suformulavimas, kurį taikant apie viską galvojama visiškai kitaip“, - sakė Kembridžo universiteto (JAV) fizikas teoretikas Davidas Skinneris
Pats amplituedras gravitacijos neaprašo. Tačiau N. Arkani-Hamedas su kolegomis mano, jog gali egzistuoti susijęs geometrinis objektas, kuris šią užduotį atlieka. Jo savybės išaiškintų, kodėl dalelės egzistuoja, kodėl jos juda trijuose erdvės matmenyse ir kinta bėgant laikui.
Kadangi „žinome, jog kažkada teks sukurti teoriją, kurioje nebūtų unitariškumo ir lokalumo, tai yra pradinis taškas siekiant galutinio ir pilno kvantinės gravitacijos teorijos aprašymo“, - sakė J. Bourjaily.
Sudėtingi skaičiavimai
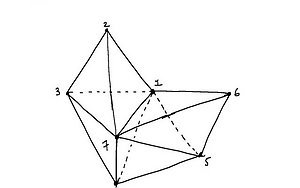
Geros vaizduotės reikalaujantis amplituedras atrodo kaip sudėtingas, brangakmenis turintis daug paviršių aukštesniuose matmenyse. Jo tūriuose yra užkoduotos pačios esminės realybės savybės, kurios gali būti apskaičiuotos - išsibarstymo amplitudės, nusakančios tikimybę, kad tam tikras dalelių rinkinys susidūrimo metu taps kitokių konkrečių dalelių rinkiniu. Tokias lygtis skaičiuoja ir labai dideliu tikslumu tikrina dalelių fizikai, dirbantys su tokiais greitintuvais, kaip LHC.

Vienas iš garsiausių XX a. fizikų, Richardas Feynmanas, sukūrė būda apskaičiuoti dalelių sąveikų tikimybes naudojant visų galimų skirtingų sąveikų aprašymus. „Feynmano diagramos“ buvo atvaizduotos JAV pašto tarnybos 2005 metų pašto ženkle, skirtame šiam mokslininkui pagerbti.
Dabar naudojamas jau 60 metų sulaukęs metodas apskaičiuoti išsibarstymo amplitudes – anuomet tai buvo galinga mokslo inovacija, išmąstyta Nobelio premijos laureato fiziko Richardo Feynmano. Jis pabraižė visų būdų, kuriais galėtų vykti išsisklaidymo procesas, eskizus ir tuomet susumavo skirtingų piešinių teisingumo tikimybes. Pačios paprasčiausios Feynmano diagramos atrodo tarsi medžiai: susidūrime dalyvaujančios dalelės susilieja tarsi šaknys, o susidarančios dalelės išsišakoja tarsi šakos. Sudėtingesnės diagramos turi kilpas, kuriose susiduriančios dalelės tampa nestebimomis „virtualiomis dalelėmis“, kurios sąveikauja tarpusavy, kol vėliau išsišakoja į tikrus galutinius produktus. Yra diagramų su viena kilpa, dviem kilpomis, trimis kilpomis ir taip toliau – vis įmantresnėmis išsibarstymo proceso iteracijomis, kurios vis mažiau prisideda prie bendros amplitudės. Virtualios dalelės gamtoje niekada nestebimos, bet buvo manoma, kad jos yra matematiškai privalomas unitariškumo elementas, mat be jų neįmanoma gauti vienetui lygios tikimybių sumos.
„Feynmano diagramų kiekis yra toks sprogstamai didelis, kad netgi labai paprastų procesų skaičiavimai nebuvo atliekami iki atsirandant kompiuteriams“, - sakė J. Bourjaily. Iš pirmo žvilgsnio paprastam įvykiui – pavyzdžiui, dviejų subatominių dalelių gluionų susidūrimui, kurio metu susidaro keturi mažiau energijos turintys gliuonai (o tai LHC greitintuve nutinka milijardus kartų per sekundę) – aprašyti reikia 220 diagramų, kurios kartu sudaro tūkstančius išsibarstymo amplitudės matematinių išraiškų.
1986 metais tapo akivaizdu, kad R. Feynnamo aparatas yra tarsi Rubio Goldbergo mašina, pačius paprasčiausius darbus atliekanti pačiu sudėtingiausiu būdu.
Ruošiantis Superlaidaus Super greitintuvo statyboms Teksaso valstijoje (vėliau šis projektas buvo atšauktas) fizikai teoretikai norėjo apskaičiuoti visų žinomų dalelių sąveikų išsibarstymo amplitudes, kad turėtų informacijos pagrindą, su kuriuo lyginant būtų akivaizdu, kurie signalai yra egzotiški, o kurie – ne. Tačiau net ir 2 gliuonų virtimo 4 gliuonais procesas buvo toks sudėtingas, kad fizikų grupė anuomet pareiškė, jog „jo įvertinimas gali būti neįmanomas numatomoje ateityje“.
Fermi nacionalinio greitintuvo laboratorijos (JAV) fizikai teoretikai Stephenas Parke'as ir Tommy Tayloras šį pareiškimą priėmė kaip iššūkį. Pasinaudoję keliomis matematinėmis gudrybėmis jie dviejų gliuonų virtimo keturiais išsibarstymo amplitudės skaičiavimus sugebėjo supaprastinti nuo kelių milijardų išraiškų iki 9 puslapių ilgio formulės, kurią galėjo sudoroti 1980 metais pagamintas superkompiuteris. Tuomet, remdamiesi kitų gliuonų sąveikų išsibarstymo amplitudžių savybėmis, S. Parke'as ir T. Tayloras spėjo paprastą vienos išraiškos lygtį amplitudei. Superkompiuteris patvirtino, kad ji buvo ekvivalentiška 9 puslapių apimties formulei. Kitaip tariant, tradicinis kvantinio lauko teorijos skaičiavimo aparatas, kuriame buvo naudojami šimtai Feynmano diagramų ir tūkstančiai matematinių išraiškų, slėpė šį tą kur kas paprastesnio. Kaip sakė J. Bourjaily, „Kam sumuoti milijonus dalykų, kai atsakymas slypi vienoje funkcijoje?“
„Tuomet žinojome, kad gavome svarbų rezultatą. Akimirksniu tai supratome. Bet ką su juo daryti?“, - pasakojo S. Parke'as.
Amplituedras
S. Parke'o ir T. Tayloro vienos išraiškos rezultato paskleistą žinią fizikai-teoretikai gliaudė dešimtmečius. „Ta viena išraiška, nuostabi nedidelė funkcija, ateinančius 30 metų buvo tarsi švyturys. Ji ir pradėjo visą šią revoliuciją“, - tikino J. Bourjaily.
Praėjusio dešimtmečio viduryje dalelių sąveikų išsibarstymo amplitudėse išaiškėjo dar viena tendencija, nepaliaujamai rodžiusi ženklus, kad egzistuoja kažkokia bazinė koherentiška struktūra, galinti nusakyti kvantinio lauko teoriją. Svarbiausias iš šių ženklų buvo formulių rinkinys, vadinamas BCFW rekursiniais santykiais – formulių rinkinys pavadintas Ruth Britto, Freddy Cachazo, Bo Fengo ir Edwardo Witteno garbei. BCFW santykiai išsibarstymo procesus aprašinėjo ne kaip puikiai pažįstamus kintamuosius, nusakančius padėtį erdvėje ir laiką ir iliustruojamus Feynmano diagramomis, o naudojant keistų kintamųjų, pavadintų „tvistoriais“, terminą. Dalelių sąveikos gali būti aprašomos vos keliomis susijusių tvistorių diagramomis. Labai greitai formulių rinkiniu pradėjo naudotis su LHC ir kitais greitintuvais dirbantys mokslininkai, skaičiavę jiems svarbias išsibarstymų amplitudes.
„Šių BCFW santykių sąvokos buvo tarsi kilę iš kito pasaulio ir norėjome suprasti koks yra tas kitas pasaulis. Todėl prieš penkerius metus ir susidomėjau šia tema“, - sakė N. Arkani-Hamedas.
Padedamas puikių matematikų, tokių, kaip Pierre'as Deligne'as, N. Arkani-Hamedas su kolegomis atrado, kad rekursiniai santykiai ir susijusių tvistorių diagramos puikiai atitiko gerai žinomą geometrinį objektą. Tiesą sakant, kaip aprašyta gruodį „arXiv.org“ publikuotame darbe, N. Arkani-Hamedas, J. Bourjaily ir kiti mokslininkai pateikė instrukcijas apskaičiuoti šio objekto, vadinamo teigiamu Grasmanianu, tam tikrų dalių tūrį.
XIX a. Vokietijos lingvisto ir matematiko Hermanno Grassmanno vardu pavadinta figūra – teigaimas Grasmanianas - „yra kiek labiau išaugęs trikampio vidaus pusbrolis“, - sakė N. Arkani-Hamedas. Trikampio vidus yra dvimatė erdvė, apribota susikertančiomis linijomis, o paprasčiausias teigiamo Grasmaniano atvejis yra N-matės erdvės regionas, ribojamas susikertančių plokštumų. N yra skaičius dalelių, dalyvaujančių išsibarstymo procese.
Tai buvo tikrų dalelių duomenų geometrinė reprezentacija, rodžiusi tikimybę, kad du susiduriantys gliuonai virs keturiais. Bet kažko vis dar trūko.
Fizikai tikėjosi, kad išsibarstymo proceso amplitudė grynai ir neišvengiamai išaiškės iš geometrijos, tačiau teigiamo Grasmaniano komponentus, kuriuos reikėjo sudėti norint gauti reikiamą rezultatą, diktavo lokalumas ir unitariškumas. Tad mokslininkams kilo klausimas – ar amplitudė yra „atsakymas į tam tikrą matematinį klausimą. Ir paaiškėjo, kad taip iš tiesų ir yra“, - sakė šio darbo bendraautoris Jaroslavas Trnka, tuomet Kalifornijos technologijos universitete vykdęs podoktorantūrinius tyrimus.
N. Arkani-Hamedas ir J. Trnka išsiaiškino, kad išsibarstymo amplitudė yra lygi visiškai naujo matematinio objekto – amplituedro – tūriui. Tam tikro išsibarstymo proceso detalės padiktuoja atitinkamo amplituedro matmenų ir paviršių kiekį. Teigiamo Grasmaniano dalys, kurios buvo apskaičiuojamos naudojant tvistorių diagramas ir tuomet sudedamos ranka,tapo statybiniais elementais, kurie sudarė amplituedrą, lygiai kaip sudūrus trikampius gaunama daugiakampė struktūra.
Kaip ir tvistorių diagramos, Feynmano diagramos yra kitoks būdas apskaičiuoti amplituedro tūrį pažingsniui, tačiau jos yra kur kas mažiau efektyvios. „Jos yra lokalinės ir unitarinės erdvėlaikyje, tačiau jos nebūtinai labai patogios ar gerai atitinka šio deimanto formą. Feynmano diagramų naudojimas yra palyginamas su Mingų dinastijos vazos paėmimu ir jos tėškimu į grindis“, - sakė D. Skinneris.
N. Arkani-Hamedas ir J. Trnka kai kuriais atvejais sugebėjo amplituedro tūrį suskaičiuoti tiesiogiai, nenaudodami tvistorių diagramų amplituedro daliniam tūriui apskaičiuoti. Jie taip pat aptiko „pagrindinį amplituedrą“ su begaliniu paviršių kiekiu, primenantį dvimatį apskritimą, kuris turi neribotą kraštinių kiekį. Teoriškai tokio amplituedro tūris atitinka bendrą visų fizikinių procesų amplitudę. Žemesnių matmenų amplituedrai, kuire atitinka sąveikas tarp baigtinio dalelių kiekio, egzistuoja pagrindinio amplituedro paviršiuose.
„Tai yra labai galingi skaičiavimo metodai, bet jie yra ir labai įtaigūs. Jie teigia, kad mąstymas erdvėlaikio ribose buvo neteisingas būdas spręsti šiuos uždavinius“, - sako D. Skinneris.
Kvantinės gravitacijos paieškos
Iš pirmo žvilgsnio neišsprendžiamas konfliktas tarp gravitacijos ir kvantinio lauko teorijos juodosiose skylėse pasiekia krizę. Juodosiose skylėse į mažutę erdvę suspaudžiami milžiniškai kiekiai masės, todėl kvantiniame lygmenyje gravitacija tampa labai svarbiu veiksniu, nors įprastinėmis sąlygomis ją būtų galima ignoruoti. Šioje situacijoje konflikto šaltinis neišvengiamai yra arba lokalumas, arba unitariškumas.
Kaip jau minėta, lokalumas ir unitariškumas yra pagrindinės kvantinio lauko teoriją laikančios kolonos, bet, kaip parodys vienas minčių eksperimentas, abi šios kolonos subyra tam tikrose situacijose, kuomet veikia gravitacija. Tai reiškia, tad fiziką reikėtų apibrėžinėti atsisakant abiejų šių principų.
Lokalumas teigia, kad dalelės sąveikauja erdvėlaikio taškuose. Bet įsivaizduokite, kad norite iš labai arti pažiūrėti į erdvėlaikio tašką. Vis mažesnių ir mažesnių atstumo mastelių stebėjimas reikalauja vis didesnės energijos, bet pasiekus tam tikrą atstumą, vadinamą Planko ilgiu, vaizdas išsilieja. Į tokį mažutį regioną reikia įsprausti tiek daug energijos, kad visa ši energija tą stebimą regioną suspaudžia į juodąją skylę, todėl stebėjimas tampa nebeįmanomu. „Nėra jokių galimybių matuoti erdvės ir laiko atstumus, kuomet jie tampa mažesniais už Planko ilgį. Taigi, įsivaizduojame, jog erdvėlaikis yra tolydus dalykas, tačiau kad jau neišeina apie tai kalbėti griežtai, vadinasi, tai nėra fundamentali savybė, ji turi būti atsirandanti“, - sakė N. Arkani-Hamedas.
Unitariškumas tvirtina, kad vykstant dalelių sąveikai visų galimų kvantinės mechanikos rezultatų tikimybių suma turi būti lygi vienetui. Norint tai įrodyti reikėtų stebėti tokią pačią sąveiką daugybę kartų ir įvertinti kiekvieno rezultato dažnumą. Šį darbą atliekant idealiu tikslumu reikėtų begalinio stebėjimų kiekio naudojant be galo didelį matavimo aparatą, tačiau ir šis sukeltų gravitacinį sugriuvimą į juodąją skylę. Baigtiniuose Visatos regionuose unitariškumas gali būti tik apytikslis.
„Turime tam tikrų ženklų, kad abiejų šių savybių reikia atsisakyti. Jos negali būti fundamentaliomis kito aprašymo – tokio, kaip kvantinės gravitacijos teorijos – savybėmis“, - sakė N. Arkani-Hamedas.
Stygų teorija, nusakanti daleles kaip neįžiūrimai mažas vibruojančias stygas yra vienas iš kandidatų tapti kvantinės gravitacijos teorija, kuri nesubliūkšta juodųjų skylių situacijose, tačiau jos santykiai su realybe yra nepatikrinti – ar bent jau gana painūs. Gana neseniai buvo aptiktas keistas dvilypumas tarp stygų ir kvantinio lauko teorijų – jis rodo, jog stygų teorija, kurioje apibrėžiama gravitacija, yra ekvivalentiška antrajai, kuri gravitacijos neapibrėžia, jeigu aprašomas įvykis vyksta skirtinguose matmenų kiekiuose. Niekas nežino kaip tokį atradimą vertinti. Tačiau naujas amplituedro tyrimas suteikia pagrindo manyto, jog erdvėlaikis, taigi, ir matmenys, gali būti tik iliuzija.
„Negalime remtis įprastiniu kvantinės mechanikos erdvėlaikio vaizdu aprašant fiziką. Reikia išmokti naujų būdų visa tai nusakyti. Mūsų darbas – nedrąsus kūdikio žingsnis šia kryptimi“, - sakė darbo vadovas.
Ir netgi atmetus unitariškumą bei lokalumą, kvantinio lauko teorijos aprašymas taikant amplituedrą dar neaprašo gravitacijos. Bet mokslininkai nesiliauja dirbti. Jie tikina, kad išsibarstymo procesus, kuriuose dalyvauja gravitacijos dalelės, galima būtų aprašyti amplituedru ar panašiu geometriniu objektu. „Jis gali būti glaudžiais susijęs su amplituedru, bet šiek tiek kitoks ir sunkiau aptinkamas“, - sakė D. Skinneris.
Fizikai taip pat turės įrodyti, kad naujoji geometrinė formuluotė yra tinkama toms pačioms dalelėms apie kurių egzistavimą Visatoje yra žinoma, o ne idealizuotai kvantinio lauko teorijai (maksimaliai supersimetriškai Yang-Mills teorijai), kuri buvo panaudota amplituedrui kurti. Ši teorija aprašo po „superpartnerį“ kiekvienai žinomai dalelei ir erdvėlaikį vertina kaip plokštumą. „Taip jau nutiko, kad tai buvo paprasčiausias bandymų poligonas visiems šiems naujiems įrankiams. Bet suprantame ir būdą generalizuoti šiuos naujus įrankius kitoms teorijoms“, - sakė J. Bourjaily.
N. Arkani-Hamedo teigimu, amplituedro atradimas gali ne tik palengvinti skaičiavimus ir galbūt nutiesti kelią į kvantinės gravitacijos teoriją. Jis gali tapti priežastimi žengti dar didesnį žingsnį – atsisakyti erdvės ir laiko kaip fundamentalių aplinkos elementų ir išsiaiškinti, kokiu būdu iš grynos geometrijos radosi Didysis sprogimas ir kosmologinė Visatos evoliucija.
„Tam tikra prasme suvoktume, kad pokyčiai kyla iš objekto struktūros. Bet objektas nesikeistų. Pats objektas yra iš esmės belaikis“, - sako mokslininkų grupės vadovas.
Ir nors šis darbas nėra iki galo pabaigtas, daugybė fizikų teoretikų į jį jau nukreipė savo akis laukdami naujų idėjų.
Pažangiųjų tyrimų instituto, kuriame savo laiku dirbo Albertas Einsteinas, Johnas van Neumannas, Kurtas Goedelis, Alanas Turingas ir kitų paties stambiausio kalibro mokslininkų, fizikas teoretikas E. Wittenas sakė: „Tai yra labai greitai besivystanti sritis ir labai sunku nuspėti kas nutiks ateityje arba ko pasimokysime“.